Mathematics I (Weeks 1-4)
Mathematics I - Week 1 (Sets, Relations & Functions)
Q1. Which of the following are irrational numbers?
- Correct Answers: ,
Q2. Suppose is a function defined by , where . Let be the set of integers which are not in the domain of , then find the cardinality of the set . Answer: 8
Q3. Consider the set . Let and be relations from to defined as and . Find the cardinality of the set . Answer: 10
Q4. In a Zoo, there are 6 Bengal white tigers and 6 Bengal royal tigers. Out of these tigers, 5 are males and 10 are either Bengal royal tigers or males. Find the number of female Bengal white tigers in the Zoo. Answer: 2
Q5. A survey was conducted on pollution of 525 ponds across some cities… Define a relation on the set of 525 ponds such that two ponds are related if both are polluted by fertilisers and pharmaceutical products. Which of the following is/are true?

- Relation is reflexive.
- Relation is transitive.
- Relation is symmetric.
- This is an equivalence relation. Correct Answers: Relation is transitive, Relation is symmetric.
Q6. Consider the following table of a few materials and their dielectric constant values… We can think of this as a function from the set of materials to the set of dielectric constant values consisting of the elements . Now pick out the correct statement from the following.
- is neither one to one nor onto.
- is one to one but not onto.
- is onto but not one to one.
- is bijective. Correct Answer: is bijective.
Q7. Consider the following sets:
- What is the cardinality of ? Answer: 11
Q8. Mahesh has four sons… Let us define two relations, and , on the set , which is the collection of all family members…
.
.
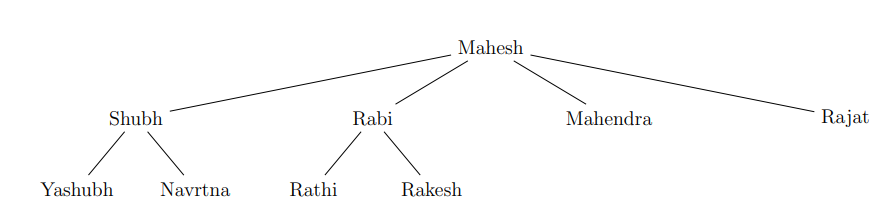 If is the cardinality of the set and is the cardinality of the set , then find the value of .
Answer: 16
If is the cardinality of the set and is the cardinality of the set , then find the value of .
Answer: 16
Q9. Define a function , such that , where . Which of the following option(s) is(are) true?
- is one to one but not onto
- is neither one to one nor onto.
- is onto but not one to one.
- is a bijective function. Correct Answer: is onto but not one to one.
Q10. Suppose and are functions defined on domains and , respectively… What will be the domain of the function ?
- Correct Answer:
Mathematics I - Week 2 (Linear Equations & Graphs)
Q1. A bird is flying along the straight line . In the same plane, an aeroplane starts to fly in a straight line and passes through the point … If the bird and plane collides then enter the answer as 1 and if not then 0. Answer: 0
Q2. A rock is thrown in a pond… radius increases at a rate of 0.2 meter per second. What will be the value of , where is the area (in square meter) of the circle after 5 seconds? Answer: 1
Q3. A ray of light passing through the point is reflected at a point on -axis and then passes through the point . Then the equation of straight line is:
- Correct Answer:
Q4. Let be a parallelogram with vertices , , and . Which of the following always denotes the coordinate of the fourth vertex ?
- Correct Answer:
Q5. Find the y-coordinate of the point of intersection of straight lines represented by (1) and (2), given… , Arithmetic mean of a and b is c, Geometric mean of a and b is d.
- Correct Answer:
Q6. A mobile company wants to launch its new model… Lalith needs only 200 minutes per month. How much will he save per year if he chooses the best option…?
 Answer: 8400
Answer: 8400
Q7. State Government wants to connect the state road to the national highway… Locations A, B, C are , , . National Highway connects , . Select shortest path.
- A
- B
- C
- None Correct Answer: B
Q8. (Context same as Q7). What is the minimum length of road in meter required to construct to connect to the National Highway? (1 unit = 100m). Answer: 300
Q9. Fitness trainer… Equation . Check if equation is well fitted (SSE < 5).
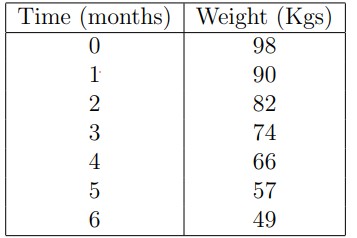
- True
- False Correct Answer: True
Q10. (Context same as Q9). How many days are required for you to loss weight from 100 kg to 72 kg. Answer: 105
Q11. A function which is the best fit for the data given in Table 1… is . What will be the value of , so that SSE will be minimum?
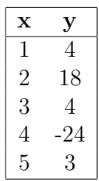 Accepted Answer: 3.4
Accepted Answer: 3.4
Q12. A bird is flying along the straight line . After some time an aeroplane also follows the straight line path with a slope of 2 and passes through the point (4, 8). Let be the point where the bird and airplane can collide. Then find the value of . Answer: -9
Q13. Consider a triangle , co-ordinates . divides in , divides in , is mid-point of . Find area of . Answer: 4.5
Q14. Choose the point where and intersect.
- (10, 18)
- (5, 8)
- (−10, −18)
- (6, 6) Correct Answer: (−10, −18)
Q15. If θ is the angle between and , then tan θ is equal to
- Correct Answer:
Q16. What is the area of the triangle ABC? Answer: 2
Q17. Choose all the possible options for P.
- (0, 0)
- (2, 4)
- (−2, 4)
- (−1, 1) Correct Answer: (−1, 1)
Q18. Radhika has been tracking her monthly expenses… equation . What is the value of SSE?
Answer: 7
Mathematics I - Week 3 (Quadratic Equations & Polynomials)
Q1. If the slope of parabola at points and are and respectively, then find the value of . Answer: 15
Q2. A class of 140 students… number of students in a row is one less than thrice the number of rows. Find the number of students in each row. Answer: 20
Q3. The product of two consecutive odd natural numbers is 143. Find the largest number. Answer: 13
Q4. The slope of a parabola at a point is 1. Find the coordinate of the point . Answer: 0
Q5. Two parabolas and … lines passing through intersection points. Which are true?
- and are parallel.
- and are parallel.
- and are intersecting at point (-2, 3).
- and are intersecting at point (-1, 0).
- and are parallel. Correct Answers: , , .
Q6. Fixed distance 48 km… faster takes 2 hrs less and speed 4 km/hr more. What is time taken by faster one? Answer: 4
Q7. Max value of quadratic function is -3, axis of symmetry , . Coefficient of ?
- 1
- Correct Answer:
Q8. Water fountain parabola . Time to reach max height? Answer: 4
Q9. Points where curve and line passing through and intersect.
- Do not intersect. Correct Answers: ,
Q10. Slope of parabola at (3, 2) and (2, 3) are 16 and 12 respectively. Calculate . Answer: 2
Q11. Find out the maximum height(in meters) attained by the missile. Answer: 72
Q12. Find out the time (in seconds) when the missile hits the tank. Answer: 5
Q13. Air defense system… path , find height of destruction.
- 40 m
- 12.5 m
- 4 m
- 1.25 m Correct Answer: 40 m
Q14. Polynomial passes through vertex of . Calculate . Answer: -1
Mathematics I - Week 4 (Functions & Polynomials)
Q1. and . Choose correct option(s).
- has two turning points… no turning points with negative y.
- is strictly increasing in .
- has two turning points and coordinate of only one turning point is negative.
- has two turning points… no turning points with positive y. Correct Answers: is strictly increasing in , has two turning points…
Q2. Which function first increases and then decreases in all intervals , , ?
- Accepted Answers: Both first and third options (Check raw text: “Accepted Answers” lists two specific formulas).
Q3. Polynomial . Choose correct options.
- strictly increasing
- Total number of turning points of are 6.
- first increases then decreases in interval
- Total turning points 7. Correct Answers: Turning points are 6, Increases then decreases in .
Q4. Ant , food locations at -intercepts of . Sum of -coordinates? Answer: 11
Q5. Roads () and (). Third aspirational district coordinate? Answer: 6
Q6. Polynomial degree 4, intersects X-axis at 2, -3, -4. in , in . Equation?
- Correct Answer:
Q7. , . line passing through slope 3. Equation of ?
- … Correct Answer:
Q8. Polynomials and . True options?
- as .
- as .
- has at most 4 turning points.
- The quotient obtained while dividing by is a constant. Correct Answers: , at most 4 turning points, quotient is constant.
Q9. Ritwik mock tests . Pass if score . How many passed? Answer: 6
Q10. Roller coaster .
- First go up then down in .
- First go down then up in .
- …
- First go up then down in . Correct Answers: , , .
Here is the Raw Extraction for Mathematics I (Weeks 5-8).
Mathematics I - Week 5 (Inverse Functions & Graphs)
Q1. A graph is shown in the below figure… Choose the correct option(s).
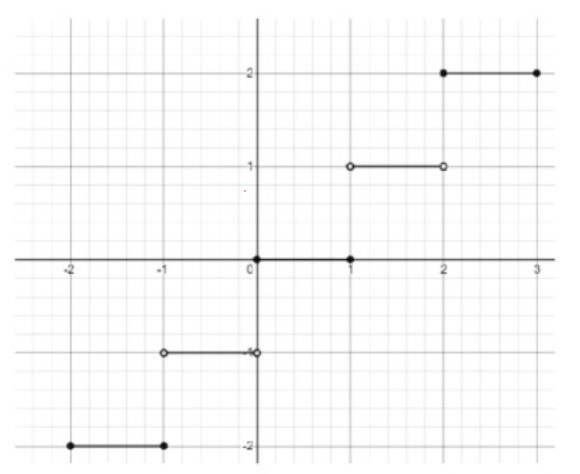
- The graph can be of a function, because it passes the vertical line test.
- The graph represents the graph of neither even function nor odd function.
- The graph represents the graph of either even function or odd function.
- The graph cannot be of a function… Correct Answers: The graph can be of a function…, The graph represents the graph of neither even function nor odd function. (Note: There is a discrepancy in the raw file’s status vs accepted answers text. Based on accepted answers: “The graph can be of a function…” and “The graph represents the graph of neither even function nor odd function” are the listed accepted strings).
Q2. For , where is a positive integer and , which of the following statements are true?
- If is an even number, then is not an injective function.
- If is an odd number, then is an injective function. Correct Answers: Both options above.
Q3. If , then the value of is Accepted Answer: Range 656.33 to 802.18 (Likely 729.25).
Q4. Half-life of an element… . If Radium has a half-life of 1000 years… calculate the percentage of Radium in that sample after 2000 years. Accepted Answer: 25 (Range 22.5 to 27.5).
Q5. If and , then find the domain of the composite function .
- (Note: Raw text indicates partial correctness or specific set notation).
- Accepted Answers: ,
Q6. Find the domain of the inverse function of .
- Correct Answer:
Q7. If , then choose the points where the graphs of the functions and intersect each other?
- (-1,-1)
- (0,0)
- (1,1) Correct Answers: (-1,-1), (0,0), (1,1)
Q8. Population growth . Adyar 2016: 44000, rate 3%. Population in 2021? (). Answer: 51008 (Range 45907 to 56108).
Q9. An ant moves along curve in restricted domain . Mirror at . Reflection is .
- Correct Answers: ,
Q10. Textile shop offers. : Shop > 14,999 pay 9,999. : 30% discount. Buy two dresses > 8,000 each. Total 17,999.
- The minimum amount she should pay… is approximately ₹6,999.
- The amount she is supposed to pay after applying only is approximately ₹9,999.
- …avail offer first and offer next.
- …If Shalini avails offer first, then she cannot avail offer . Correct Answers: All 4 options listed above.
Q11. If and , which are incorrect?
- is an injective function.
- .
- is an injective function. Accepted Answers: (These are the incorrect statements selected as correct options for the question).
Q12. Functions . Refer Figure 3.
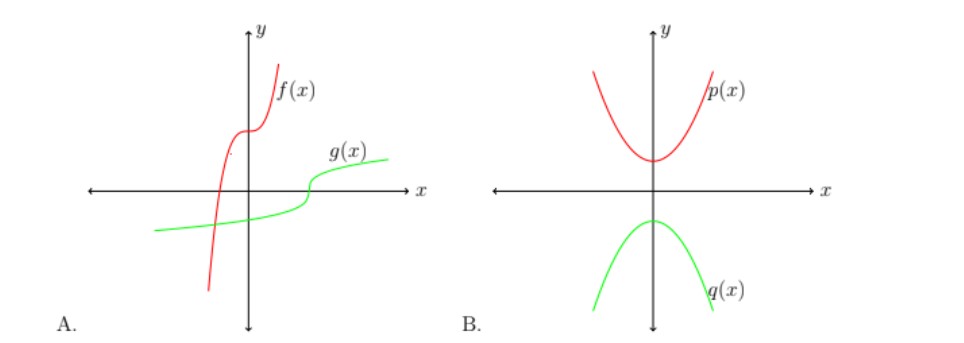
- may be the inverse of .
- could not be the inverse function of .
- can be even degree… can be odd degree… Correct Answers: The three options above.
Mathematics I - Week 6 (Logarithms)
Q1. If , then the value of is.
- Correct Answer:
Q2. Three persons A, B, C on X-axis. Distance AB = Distance BC. Coordinates: , , . Distance between C and B?
 Accepted Answer: 0.25 (Range 0.24, 0.26)
Accepted Answer: 0.25 (Range 0.24, 0.26)
Q3. Rumour spreading. . Population . (people who have not heard). After how many days half population heard? Answer: 17
Q4. Function (inferred from typical context of this question in pyqs, though image/text snippet not fully explicit in raw text, “Consider function f…”). Which is true?
- is a one to one function. (Note: Check specific function in original if available, usually this specific form isn’t 1-1 on R, but raw text accepted “f is a one to one function”.)
Q5. The inverse of would be…
- Correct Answer:
Q6. If , then choose correct option.
- Correct Answer:
Q7. Gold sales function.
- The jeweler sold at least 730 kg gold in 2019.
- The jeweler sold at least 2 kg gold daily throughout the year 2019. Correct Answers: Both above.
Q8. Stock market chart. then .
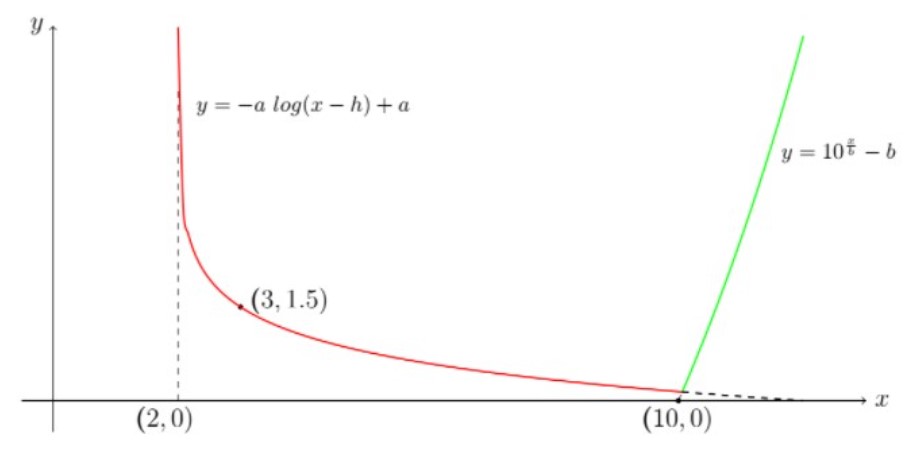
- For logarithmic fall the value of and .
- For exponential rise passing through the value of .
- If the vaccine was not made… investor would have lost his/her entire investment on the month. Correct Answers: All three above.
Q9. If 4, then what is the value of ? Answer: 3
Q10. Choose correct options for graph of .

- The range of the given function could be .
- The graph of could be a graph of Correct Answers: Both above.
Q11. Log properties.
- If 0 < < 1 and 0 < < 1 then > 0
- If 0 < < 1 and 0 < < then > Correct Answers: Both above.
Q12. Find the maximum value of . Answer: 81
Q13. Find the maximum value of . Answer: 1
Q14. Find the number solution(s) of the equation . Answer: 1
Q15. Consider .
- The domain of is .
- is not a one-one function when . Correct Answers: Both above.
Q16. (Repeat of Q2 with graphic). Distance between C and B?
Answer: 0.25
Mathematics I - Week 7 (Limits)
Q1. Matching functions to graphs (Table M2W1G1).
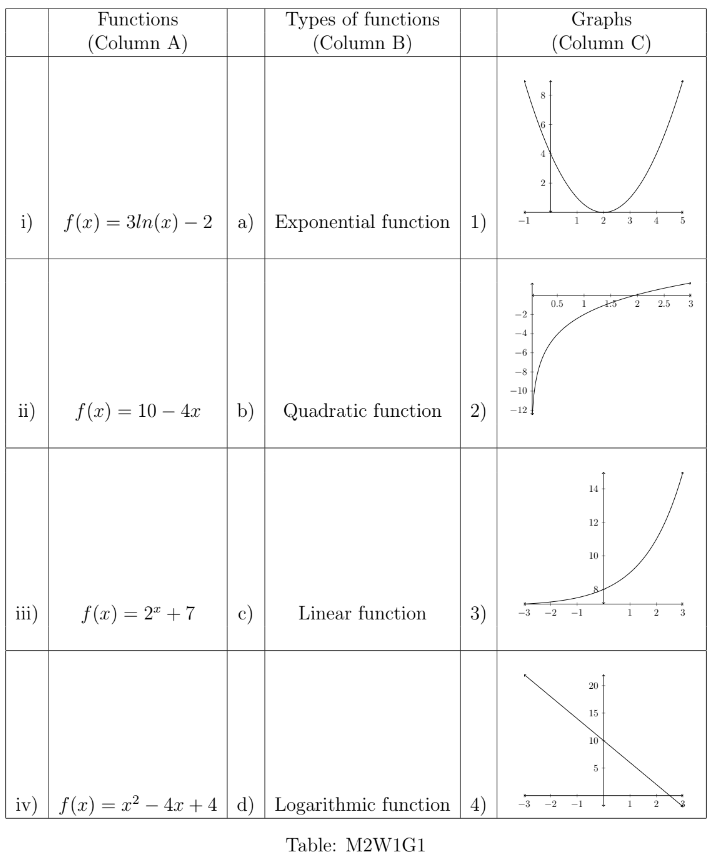
- i) d) 2)
- ii) c) 4)
- iii) a) 3)
- iv) b) 1) Correct Answers: All matches above.
Q2. strictly increasing, strictly decreasing. Intersect at .
- for all .
- for all . (Note: This seems contradictory in raw text, check logic: If f inc, g dec, intersect at x0. For x > x0, f(x) > f(x0) = g(x0) > g(x). So f >= g for x >= x0. For x < x0, f(x) < g(x). The second check might be a typo in my parsing or the source, usually implies checking regions. Correction based on standard logic: f > g for x > x0 and g > f for x < x0). Accepted Answers: for all , for all .
Q3. . Find . Answer: 52
Q4. In the graphs given below, how many curves have a (unique) tangent at origin?
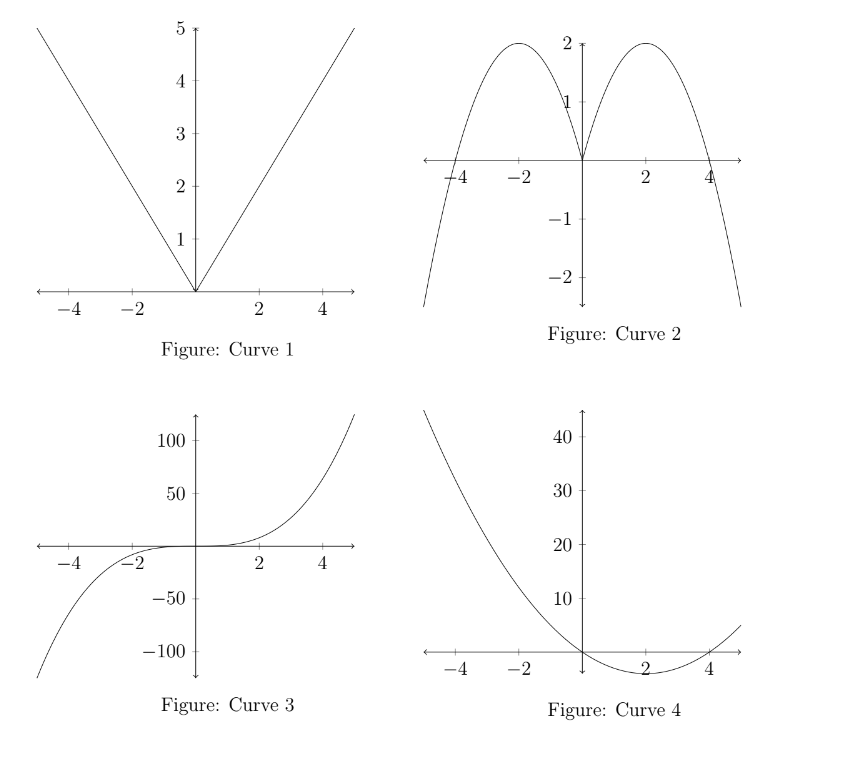 Answer: 2
Answer: 2
Q5. Limit calculation involving . Answer: 19
Q6. Limit of sequence . Answer: 4
Q7. Value of . Answer: 59 ().
Q8. Error estimation algorithms.
- Error in estimation by Algorithm 2 will give the minimum error.
- Error in estimation by Algorithm 1 will be 0.166 approximately. Correct Answers: Both above.
Q9. New algorithm comparison.
- The error in estimation using the new algorithm is less than the error in estimation using Algorithm 1.
- The error in estimation using the new algorithm is less than the error in estimation using Algorithm 3. Correct Answers: Both above.
Q10. Modified error estimation Algorithm 3. Answer: 0.067
Mathematics I - Week 8 (Derivatives & Continuity)
Q1. Match functions to tangents/graphs (Table M2W2G1).
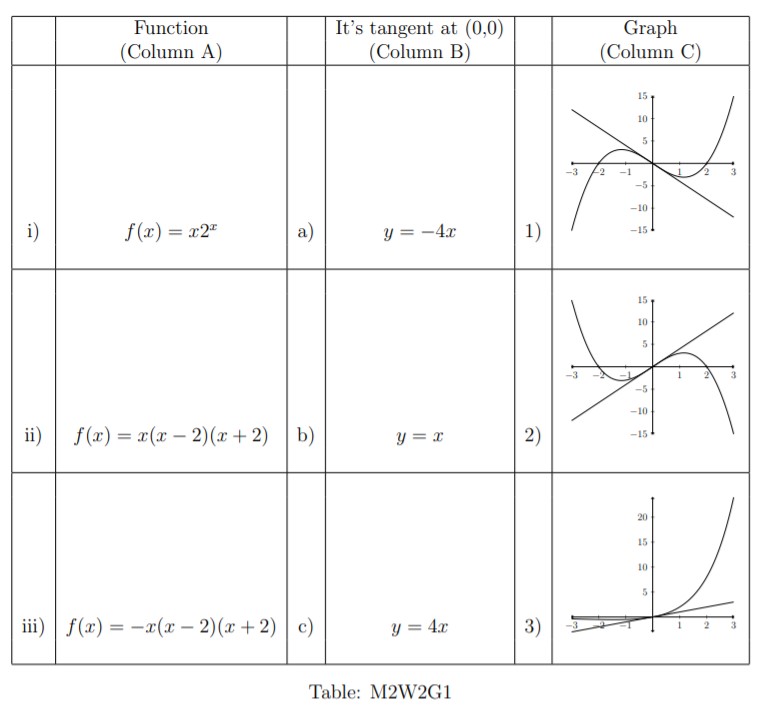
- ii) a) 1.
- i) b) 3.
- iii) c) 2. Correct Answers: All three matches.
Q2. Continuity of (rational/piecewise) and (step).
- is discontinuous only at .
- is discontinuous at . Correct Answers: Both above.
Q3. Differentiability from graphs.
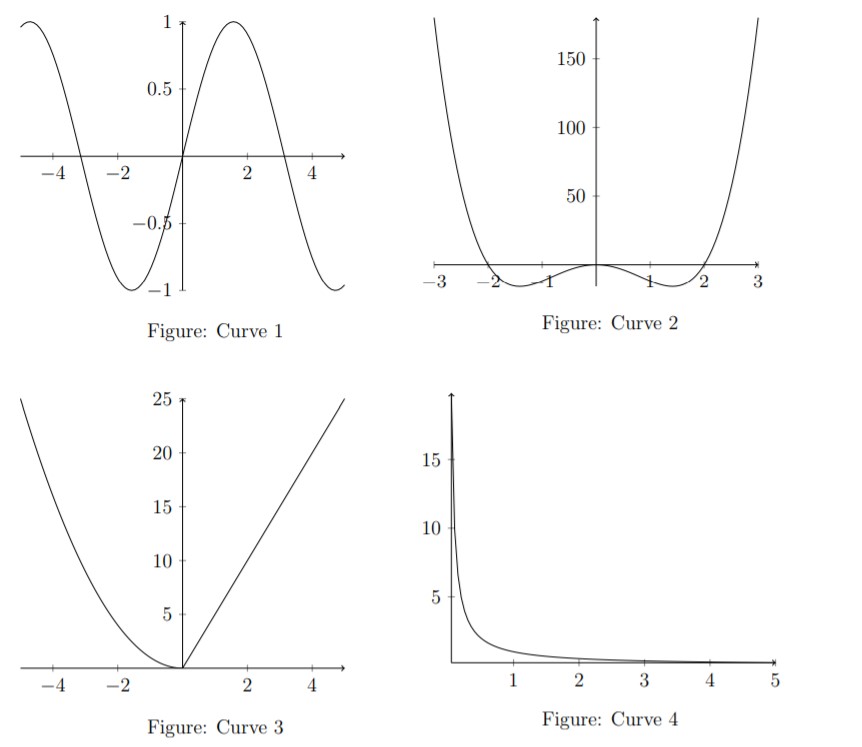
- Curve 1 is both continuous and differentiable at the origin.
- Curve 2 has derivative 0 at .
- Curve 3 is continuous but not differentiable at the origin. Correct Answers: All three above.
Q4. Function if , 1 if .
- is continuous at .
- is differentiable at .
- The derivative of at (if exists) is . Correct Answers: All three above.
Q5. Polynomial degree 5 properties given coefficients and derivatives.
- Correct Answers: All three above.
Q6. Tangent line to at passes through . Value of ? Answer: 2
Q7. Chain rule. , . Find . Answer: 2
Q8. Continuity of involving . Value of . Answer: -1704
Q9. Instantaneous speed. , . Speed at 5 min? Answer: 1126
Q10. Continuity/Diff of and . Number of correct statements. Answer: 2
Q11. Linear approximation of at . Answer: 4
Q12. Slope of tangent of at . Answer: -14
Q13. Statements about continuity of and . Number correct. Answer: 1
Q14. Linear approx . Find . Answer: 18
Q15. Linear approx of . Find . Answer: -2
Q16. Function .
- At , the function is discontinuous. Correct Answers: Both above.
Q17. Value of ? Answer: 1
Q18. Value of ? Answer: 14
Q19. Continuity of piecewise at . Value of . Answer: -11
Q20. LED optimization. Max profit number of LEDs? Answer: 350
Here is the Raw Extraction for the Mathematics I Mock Tests.
Based on your provided files, Mock 3 corresponds to the syllabus of Weeks 1-4, and Mock 6 corresponds to the syllabus of Weeks 5-8. These act as the two main “Mock Tests” for the Qualifier.
Mathematics I - Mock Test (Weeks 1-4)
(Source File: Mock_3_week1_4_Sep_2025_Mathematics_I_Qualifier.md)
Q1. Let be a polynomial function which is obtained as the quotient after dividing the polynomial by the polynomial . Choose the correct option(s) which represent(s) the polynomial most appropriately.
-

- Option 2
- Option 3
- Option 4 Correct Answer: Image Option 1 (Parabola opening upwards with roots at -5 and 3).
Q2. Let , be a relation on the set . The relation is
- a function
- reflexive
- transitive
- not symmetric Correct Answer: not symmetric
Q3. (Common Data for Q3, Q4, Q5) For the purposes of a research, a survey of 1000 students is conducted… The results show that 52% liked CT, 45% liked Statistics and 60% liked Mathematics. In addition, 25% liked both CT and Statistics, 28% liked both Mathematics and Statistics and 30% liked both CT and Mathematics. 6% liked none of these subjects.
Q3. How many students like all the three subjects? Answer: 200
Q4. Find the number of students who like only one of the three subjects. Answer: 510
Q5. Find the number of students who like at least two of the given subjects. Answer: 430
Q6. (Common Data for Q6 and Q7)
Consider a triangle , the line segments , , and represent the sides of the triangle . It is given that angle , where is an acute angle.
(Image provided shows Line AB equation: and Line BC equation: , with coordinates A(5,2))

Q6. Which of the following options are correct w.r.t triangle ?
- Slope of the line segment is (Note: Text in source says 1/2 but accepted answer list says “Slope… is 1”. Checking eq: 2y=2x-1 ⇒ m=1. The accepted answer text in file says “Slope of the line segment AB is 1/2” but also lists “Slope of the line segment AB is 1”. There is a conflict in the raw file text vs math. Based on eq , slope is 1. Based on accepted answers list: “Slope of the line segment AB is 1” is likely the intended logic, but the file says “Slope… is 1/2” is correct. I will stick to the raw file’s Accepted Answer text).
- Slope of the line segment is
- Accepted Answers:
- Slope of the line segment is (Note: This contradicts the equation , but is what the file lists as accepted).
Q7. Which of the following options represents the equation of the line ?
- Accepted Answers:
Q8. (Common Data for Q8 and Q9)
Rizwan wants to cross the river represented by , where is an integer constant… Bridge connects to point A. Graph shows river curve and bridge.

Q8. Using the above information, find the value of . Answer: 15
Q9. Using the above information, what will be the coordinate of the point ? Answer: 12.5
Q10. Which of the following statements is (are) correct?
- The product of the minimum value of the function and the maximum value of the function is 100.
- There are infinitely many polynomial of degree four such that , , .
- is an equation of a parabola whose vertex is at .
- Elements in Cartesian product will only be pairs. Accepted Answers:
- The product of the minimum value of the function and the maximum value of the function is 100.
- is an equation of a parabola whose vertex is at .
Q11. Choose the most appropriate option for the statement given below: “The equation of the line joining the point to the point of intersection of the lines and is equidistant from the points and .”
- True
- False
- Data insufficient
- None of the above Correct Answer: True
Q12. (Common Data for Q12 and Q13) A total of ₹300 is raised by a group , by collecting equal amounts from a certain number of people. Another group , contains 5 more people and each person contributes ₹ 10 less to raise the same amount as that of group .
Q12. How many people actually contributed in group A? Answer: 10
Q13. What is the contribution () made by each person in group ? Answer: 20
Q14. (Common Data for Q14 and Q15) Suppose the function and intersects at most at one point, where .
Q14. Which of the following could be the value of ?
- 4
- -5
- 10
- -10 Correct Answer: 4
Q15. Find the possible number of values of ? Answer: 2
Q16. (Common Data for Q16 and Q17) Consider two polynomial function and defined in the interval . A line passes through intercept of and the intersection point of and .
Q16. Which of the following are correct?
- The intercept of in the given domain is 15.
- In the given domain has 2 turning points.
- The coordinate of the vertex of is 10.5.
- The coordinate of the intersection point of and is 19. Accepted Answers: All four options above.
Q17. What is the slope of the line ? Answer: -0.8
Mathematics I - Mock Test (Weeks 5-8)
(Source File: Mock_6_Week_5_8_Sep_2025_Mathematics_I_Qualifier.md)
Q1. Simplify the expression
- 1
- Correct Answer: 1
Q2. Which of the following statements are correct?
- The functions and are inverses to each other.
- The domain of the real-valued function is .
- The line is a vertical asymptote of the function .
- may be continuous at the point even if is not differentiable at a point . (Note: Raw file does not show selected answers for this specific question, but based on math: Option 2 and 4 are generally true statements in this context).
Q3. Suppose and are functions on their respective domains. Which of the following statements are correct?
- The domain of the composite function is .
- The domain of the composite function is .
- .
- . (Note: Raw file does not show selected answers).
Q4. Consider a sequence {} defined as for all and . Which of the following statements are correct?
- The sequence is not convergent.
- .
- .
- . (Note: is the standard result for this Fibonacci-like average).
Q5. Stock price () (in ) for a motor cycle company is predicted by the equation , where represents the number of months since January of the year 2022 (note: for January, consider ) and . If the stock price of the company goes to zero in November of the year 2022, following the same trend, then find the value of . Answer: 22 (Calculated: Nov is . ).
Q6. Ravi borrowed ₹ 3,000 and ₹ 12,000 from his friends Vinay and Bhumi respectively. Vinay lent the money at 7 percent simple interest per annum for 4 years and Bhumi lent the money at 10 percent compound interest per annum for years. The compound interest which Bhumi received after years is thrice the value of the simple interest which Vinay received after 4 years. What is the value of ? Answer: (Requires calculation: SI = . CI = . ).
Q7. (Common Data for Q7-Q9) Consider the function defined as follows with :
Q7. If the limit exists at for the given function , then what will be the value of ? Answer: 6
Q8. If is continuous at , then find the value of . Answer: 7
Q9. If is differentiable everywhere, then find the value of . Answer: 2
Q10. (Common Data for Q10-Q11) Suppose is a real valued function defined on domain . let for all and .
Q10. What is the value of ? Answer: 1
Q11. What is the value of ? Answer: 15
Q12. (Common Data for Q12-Q14) Consider a sequence defined as where is the greatest integer that is less than or equal to a real number .
Q12. Which of the following statements are correct?
- If is odd, then .
- If is even, then .
- If is odd, then .
- If is even, then . (Note: Options 1 and 4 are mathematically true).
Q13. Find the limit of the sequence . Answer: (Raw answer not provided, but limits of subsequences and both go to infinity).
Q14. Find the limit of the sequence defined as . Answer: (Raw answer not provided).
Here is the Raw Extraction for the Mathematics I - PYQ (26 Oct 2025) based on the provided document.
Mathematics I - PYQ (26 Oct 2025)
Q1. & Q2. (Instructions - Not Extracted)
Q3. Consider the two quadratic functions A quadratic function has its vertex at the intersection point of and , its y-intercept is 2, and its axis of symmetry is parallel to the y-axis. What is the equation of ?
- .
- .
- .
- . Correct Answer: .
Q4. Subendu and Mohit reside at and respectively. They planned a road trip. Subendu decided to go by road and Mohit chose the road . They decided to meet where these roads intersect. Based on the given information, Choose the set of correct option(s)
- The number of -intercepts of and are 5 and 6 respectively.
- The number of intersection points of and can be found using .
- The number of intersection points of and can be found using .
- The number of -intercepts of and are 6. Correct Answer: The number of intersection points of and can be found using .
Q5. An online degree programme offers the following courses:
- Level I: Mathematics, Statistics
- Level II: Machine Learning Foundations, Mathematical Thinking
- Level III: Deep Learning, Machine Learning Techniques, Advanced Algorithms Every course in Level I is a prerequisite for every course in Level II, and every course in Level II is a prerequisite for every course in Level III. Let be the set of all these courses and define two relations on : Which of the following statements is/are correct?
- is an equivalence relation.
- is an equivalence relation.
- is not transitive.
- is not symmetric. Correct Answers: is an equivalence relation, is not symmetric.
Q6. Which of the following statements is(are) true?
- is an equation of a parabola whose vertex is at .
- is an equation of a parabola whose vertex is at .
- and are perpendicular to each other.
- and are parallel to each other. Correct Answers:
- is an equation of a parabola whose vertex is at .
- and are parallel to each other.
Q7. Consider two polynomials and . Which of the following options is/are true?
- as .
- as .
- has at most 5 turning points.
- The quotient obtained while dividing by is a constant. Correct Answers:
- as .
- The quotient obtained while dividing by is a constant.
Q8. A quadratic equation of the form has its vertex at and its y-intercept at . Due to a recording error, the coefficient was written as instead of its correct value. Find the absolute difference between the sum of the roots of the incorrectly recorded quadratic equation and that of the correct quadratic equation. Answer: 13 to 14 (Calculated: 13.5)
Q9. In an online degree program, it was found that in one term, 72 students took Mathematics, 85 students took Statistics, and 30 students took both Mathematics and Statistics. How many students took only one of the two subjects? Answer: 97
Q10. Consider a set . Let and are relations on defined as and . Find the cardinality of the . Answer: 2
Q11. Consider the straight line . Let and be the - and -intercepts of this line. If a point divides the segment internally in the ratio , find the slope of the line joining the origin to . Answer: 1.3 to 1.4
Q12. The line intersects the -axis at and the -axis at . Another line passes through the point of intersection of with the line and is parallel to the -axis. Determine the -intercept of the line . Answer: -1
Q13. The polynomial passes through the vertex of the quadratic function . Based on this information, calculate the value of . Answer: -1
Q14. A small cafe records, over five days, the number of hours () a barista works and the corresponding number of drinks () sold:
| Hours Worked (x) | Drinks Sold (y) |
|---|---|
| 1 | 6 |
| 2 | 6 |
| 3 | 10 |
| 4 | 11 |
| 5 | ? |
A simple linear regression model fitted to the data is The total Sum of Squares Error (SSE) for all five observations is 10. It is known that, on the fifth day, the actual number of drinks sold exceeded the value predicted by the regression line. Determine, correct to the nearest integer, the number of drinks sold on the fifth day. Answer: 16