mq3-Graded_Assignment_Sep_2025_Mathematics_I_Qualifier (3)

Graded Assignment - (Sep 2025 - Mathematics I - Qualifier)

Due date for this assignment: 2025-12-19, 23:59 IST. You may submit any number of times before the due date. The final submission will be considered for grading.

---

Question 1

Find out the equation of the curve followed by the firework.

• $y-15=-\frac{1}{15}{x}^2$
• $y-15=-\frac{1}{15}(x-15{)}^2$
• $y-30=-\frac{1}{30}(x-30{)}^2$
• $y-30=-\frac{1}{30}{x}^2$

---

Question 2

Find out the equation of the curve followed by the ball.

• $y-15=-\frac{15}{20}(x-15{)}^2$
• $y-20=-\frac{1}{20^2}{x}^2$
• $y-20=-\frac{15}{20^2}{x}^2$
• $y-15=-\frac{15}{20^2}{x}^2$

---

Question 3

If both the tasks are performed at the same time, find out the horizontal distance of the meeting point from the pole, assuming they are meeting at a point as shown in the figure. Your Answer: (Not answered)

---

Question 4

Choose the option(s) which has the most possible representation of the graph of a function $f(x).$

• $f(x)=-\log (-x^2-14x-45)$
• $f(x)=-\log (-x^2+14x-45)$
• $f(x)=-\log (x^2+14x+45)$
• $f(x)=\log (-x^2-14x-45)$

---

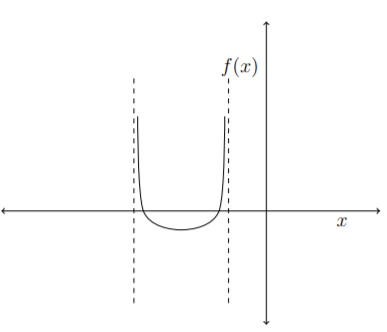
Question 5

Let $X$ be the set of natural numbers divisible by $100$, $Y$ be the set of natural numbers divisible by $25$, $Z$ be the set of natural numbers which are perfect squares. Now consider the following Venn diagram. [Note: A, B, C, D, E, F, G are the region marked in the following Venn diagram (A region in the Venn-diagram can be an empty). For example, $A=X\setminus (Y\cup Z)$, $B=Y\setminus (X\cup Z)$, and $C=Z\setminus (X\cup Y)$.

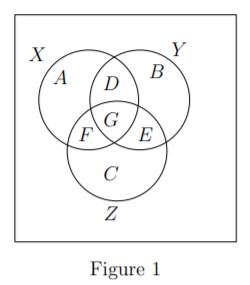
Choose the correct option(s) from below.

• $625$ is in $E$.
• $200$ is in $G$.
• $2500$ is in $G$.
• $25$ is in $F$.
• $A$ and $F$ are empty.

---

Question 6

Define the following sets,

• $S_1=\{x\mid x\in \mathbb{R},x^2+10=0\}$
• $S_2=\{x\mid x\in \mathbb{R},x^2-10=0\}$
• $S_3=\{x\mid x\in \mathbb{Q},(x^2-10)(x^2-100)=0\}$

 What is the cardinality of the set $S_1\cap S_2\cap S_3$ ? Your Answer: (Not answered)

---

Question 7

Which of the following statement are correct.

• The domain of $f(x)=\frac{1}{\left(\sqrt{-\left(x+4\right)\left(x-2\right)\left(x+2\right)\left(x-4\right)}\right)}$ is $(-4,-2)\cup (2,4).$
• If $f(x)=8$ and $g(x)=8$ then $f$ and $g$ are inverses of themselves.
• $-x^{100}$ has 1 saddle point.
• If the polynomials $x^3+a{x}^2+2x+5$ and $x^3+2x^2+3x+2a$ leave the same remainder when divided by $(x-5)$, then the value of $a$ is $\frac{-3}{2}$

---

Question 8

Parvathi launches her new company in the year 2010, which makes yearly profit in lakhs as the quadratic function $P(x)$ for first 10 years since the launch, where $x$ is the number of years after since 2010 (i.e., $x=0$ denotes the year 2010, $x=1$ denotes the year 2011, and so on). Let the loss be represented as $-ve$ of profit. Suppose in the year 2012 and 2014 the company had made neither profit nor loss, and in the year 2020 the company has been making profit. Which of the following options are correct?

• From the given information, the profit made by the company in the year 2010 cannot be determined.
• In the first ten years, the company made a loss in the year 2013 only.
• From the given information, the year(s) for which the company made loss(es) cannot be determined.
• From the given information, the year(s) for which the company made loss(es) cannot be determined.

---

Question 9

Choose the correct options from the following?

• For given $x$, $P_A\ge P_B$ is always true.
• For given $x$, $P_A\le P_B$ is always true.
• Initially the production of factory $A$ was increasing while the production of factory $B$ was decreasing.
• The production of factory $A$ and $B$ are equal for two different months.

---

Question 10

In which month $(x)$ the production of both the factories are equal? Your Answer: (Not answered)

---

Question 11

Which of the following option(s) is(are) true?

• $\underset{x\to 2^{+}}{\lim }f(x)=f(2)$.
• $\underset{x\to 2^{-}}{\lim }f(x)=f(2)$.
• $f$ is continuous at $x=2$.
• $f$ is differentiable at $x=2$.
• $f^{\prime }(3)=f^{\prime }(-3)=1$.
• $f$ is not differentiable at $x=1$.

---

Question 12

Choose the set of correct options about estimating the area of the region bounded by the graph of function $f$, in the interval $\text{[0,3]}$ using Riemann sums.

• Estimated area will be 0 sq unit, by taking 3 subintervals of equal length and the left end points of the subintervals for the height of the rectangles.
• Estimated area will be -2 sq unit, by taking 3 subintervals of equal length and the left end points of the subintervals for the height of the rectangles.
• Estimated area will be $\frac{1}{2}$ sq unit, by taking 3 subintervals of equal length and the mid points points of the subintervals for the height of the rectangles.
• Estimated area will be $\frac{5}{2}$ sq unit, by taking 3 subintervals of equal length and the mid points points of the subintervals for the height of the rectangles.

---

Question 13

Consider a function $f(x)$ defined as $f(x)=|x(x-3)|$ in the domain [-4,4]. Then which of the following option(s) is (are) true?

• The number of critical points is 3.
• The number of discontinuities of $f(x)$ is 2.
• The number of points where $f(x)$ is not differentiable is 2.
• $x=0$ is a critical point.
• The maximum value of $f(x)$ is $\frac{9}{4}$.
• The minimum value of $f(x)$ is -1.
• The number of points where $f(x)$ attains its global maximum value is 3.

---

Question 14

Let $f(x)=x(x-2)$ and $F(x)$ be the anti-derivative of $f(x)$ defined as $F(x)={\int }_{-1}^{x}f(t)dt$. Choose the set of correct options about estimating the ${\int }_{-1}^{a}f(t)dt$ on the interval [-1, $a$] using Riemann sums, where $a$ is a critical point of $F(x)$.

 [$\text{Hint:}$ Use $1^2+2^2+\dots +(n-1{)}^2+n^2=\frac{n(n+1)(2n+1)}{6}$ and $1+2+3+4+\dots +n=\frac{n(n+1)}{2}$

• If $F(x)$ has a local maximum at $x=a$, then the value of the left Riemann sum using a partition of $[-1,a]$ into two sub-intervals of equal length is $\frac{5}{8}$.
• If $F(x)$ has a local minimum at $x=a$, then the value of the right Riemann sum using a partition of $[-1,a]$ into three sub-intervals of equal length is $-1.$
• Suppose $F(x)$ has a local maximum at $x=a$. Then the limit as $n$ tends to $\infty$ of the values of the left Riemann sums using a partition of $[-1,a]$ into $n$ sub-intervals of equal length is $\frac{4}{3}$.
• Suppose $F(x)$ has a local minimum at $x=a$. Then the limit as $n$ tends to $\infty$ of the values of the right Riemann sums using a partition of $[-1,a]$ into $n$ sub-intervals of equal length is $4$.

---

Question 15

What is the weight of a minimum cost spanning tree of the graph given below?

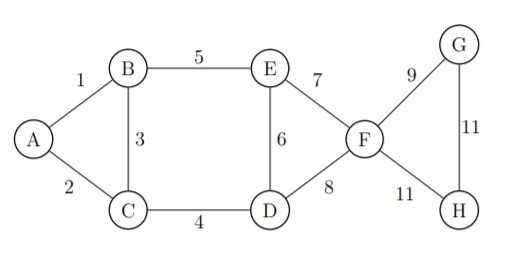Your Answer: (Not answered)

---

Question 16

A company has branches in each of six cities $C_1,C_2,....,C_6$. Let a relation $R$ is defined as

1. R=\{(a,b,c)| \text{there is a direct flight between} a \text{and} b, a \neq b, \text{with a fare of \rupee} ~c\}
2. $\text{If}(a,b,c)\in R,\text{then}(b,a,c)\in R$

An employee of that company wanted to travel from the city $C_2$ to the city $C_4$. If he traveled by the cheapest route possible, then find the total fare, he should be pay. Given that in relation$R$,

1. $(C_1,C_2,4005),(C_1,C_5,5005),(C_1,C_6,6005)\in R$
2. $(C_2,C_3,5005)\in R$
3. $(C_3,C_4,7005)\in R$
4. $(C_4,C_5,4005)\in R$
5. $(C_5,C_6,6005)\in R$ Your Answer: (Not answered)

---

Question 17

Employees of the IITM Online Degree Program are assigned to visit the exam centers in Chennai. Vidya has been asked to arrange cabs for these employees to drop them at the centers. She has created a graph (shown below) and asked Sanaya to arrange the minimum number of cabs, but has forgotten to tell Sanaya what the nodes and the edges represent. Sanaya has assumed the following cases and found the answers accordingly.

$\text{Cases:}$

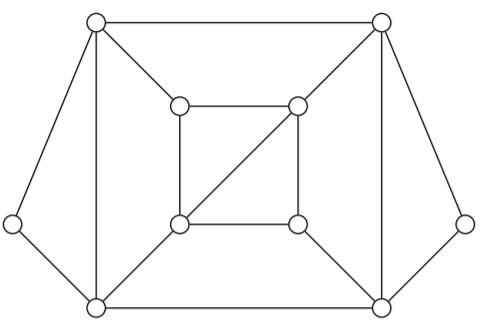
$\text{Case 1:}$ Nodes represent the locations of employees and edges represent the roads connecting these locations. Each cab can pick up employees from only one location. Sanaya needs to arrange the minimum number of cabs under the assumption that each employee is willing to walk at most one road length from their current location to a neighboring location to be picked up.

$\text{Case 2:}$ Nodes represent the employees and if two employees share an edge, then they are assigned different centers. Now, Sanaya needs to arrange the minimum number of cabs such that no two employees assigned for different centers should come in the same cab. (Assume that any number of employees can come in a cab.)
 
Choose the correct option(s).

• Case 1 would be solved by finding the maximum number of elements in independent set.
• According to case 1, the minimum number of cabs required would be 3.
• According to case 2, the minimum number of cabs required would be 3.
• Case 2 would be solved by finding the minimum number of elements in vertex cover set.

---